Most modeling attempts for modeling granular flows concern quasi-static deformations of granular materials, which are assumed be rate- independent. However, the flow of granular matter is common in the transport of granular materials such as minerals and cereals, as well as at larger scales of rock avalanches, debris flows, and other geological surface processes. Bagnold was the first to model granular flows by considering grains of average size d and density ρ subjected to a controlled shear flow of rate γ at constant volume. With these parameters, a dimensional analysis implies that the shear stress τ is proportional to ρ (dγ)^2 with a prefactor depending on the packing fraction φ (Bagnold 1954).

Inertial shear flow simulated by E. Azéma. The force chains and stress-bearing particles are shown in black and violet, respectively.
For a long time, the scaling of shear stress as γ^2 was considered to be a consequence of momentum exchange whose average value and frequency are proportional to the shear rate. This scaling was incorporated in a general theory of rapid granular flows, but its applicability to dense granular flows remained questionable as most flows encountered in practice are both frictional and collisional (Hutter and Scheiwiller 1983; Campbell 1990). The general theory of collisional granular materials was developed using the classical formalism of kinetic theory and by introducing a granular temperature T, defined as the mean square of nonaffine (or fluctuating) particle velocities, and by introducing a dissipation term through restitution coefficients for mass conservation (Jenkins and Savage 1983). In this theory, all stresses are of kinetic origin. It should also be recalled that the reference physical system in both rapid flows and granular gases has been constant-volume shear, and the rheology is described by normal and shear viscosities η_n and η_t, respectively, defined by p=η_n γ and τ=η_t γ. It was only in 2004 that it became clear that frictional and inertial flows can be described in the same framework if the volume as control parameter is replaced by the confining pressure p (GDR-MiDi 2004). The relevant dimensionless number is then the inertial number I. This number is the ratio of the internal relaxation time of the grains to the shear time. At low values of I, typically below 0.001, the flow is rate-independent. At higher values of I, the bulk friction coefficient μ increases with I whereas the packing fraction decreases. Phenomenological laws μ(I) and φ(I) for steady granular flows in combination with continuum conservation equations correctly predict the velocity and stress fields in various flow geometries (da Cruz et al. 2005; Jop et al. 2006). The increase of μ with I despite an increasingly lower packing fraction reveals a genuine microstructure. As I increases, the force chains become more sparse, the correlation length of connected particles decreases, the contact lifetimes decline, and an increasing number of impulsive forces and frictionally mobilized contacts come into play. It has been shown that the main mechanism for the increase of μ with the inertial number in inertial flows is contact anisotropy (Azéma and Radjai 2014).
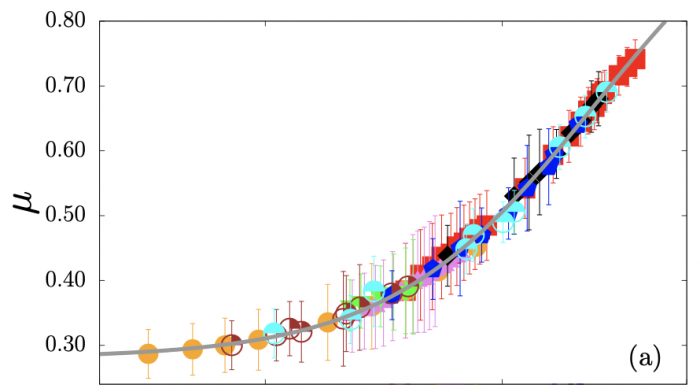
Apparent friction coefficient as a function of the inertial number in a submerged granular material.
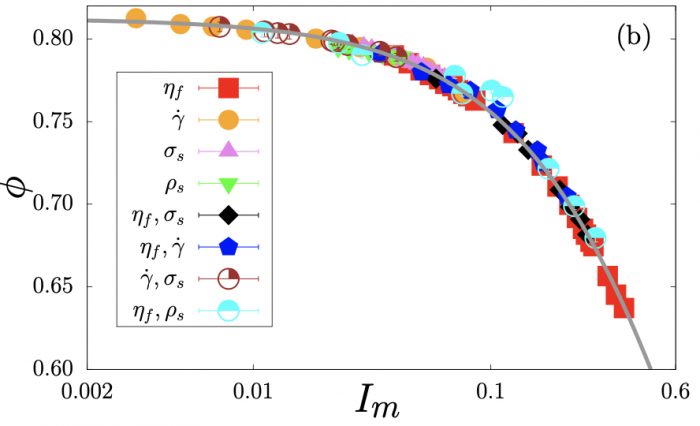
Packing fraction as a function of the inertial number in a submerged granular material. Simulations by L. Amarsid.
In the I-based rheology, μ(I) and φ(I) are the main variables. However, using the definition of I, it is straightforward to obtain the φ-based rheology (constant volume) with η_n=I^(-2) and η_t=μ(I)I^(-2). Using the experimental data with pressure-controlled flows, it was shown that both viscosities diverge as (φ_c −φ)^(−α), with α≃2, when I→0, corresponding to φ→φ_c (Boyer et al. 2011). The value of φ_c is ≃0.59 for spherical particles of the same size and coincides with the critical-state packing fraction at low confining pressures. A similar divergence is observed in dense suspensions. This indicates that the same framework may be used to unify dense granular flows and dense viscous suspensions by accounting for viscous forces as well as inertial and frictional forces (Amarsid et al. 2017). Then, the inertial number should be extended to account for the Stokes number St. This was established by means of extensive simulations using the coupled DEM-LBM method.

Inertial flow of submerged particles simulated by L. Amarsid.
A similar consideration applied to cohesive granular materials in which the inertial stress or characteristic time should be compared to a combination of both confining pressure and internal cohesive stress induced by cohesive contacts (Berger et al. 2016).
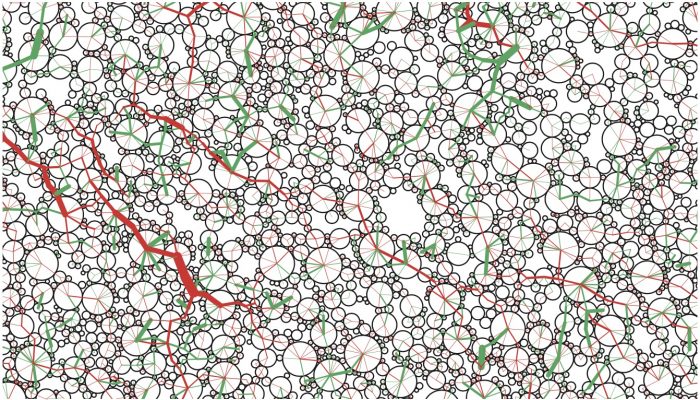
Force chains (red for compressive and green for tensile) in inertial flow of cohesive particles simulated by N. Berger.
